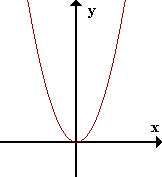
 | f(x)=x2 |
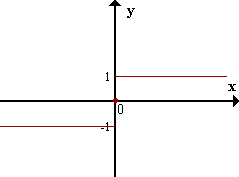 | |
La continuidad de la función f(x) para un valor a significa que f(x) difiere arbitrariamente poco del valor f(a) cuando x está suficientemente cerca de a.
Expresemos esto en términos del concepto de límite...
Definición
Continuidad
Una función f(x) es continua en un punto a si limx->af(x) = f(a).
Nota: observar que debe existir f(a) y debe existir el Ejemplos de discontinuidad
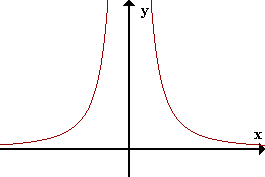 | f(x)= 1/x2 Discontinua en x=0 (No existe f(0)) |
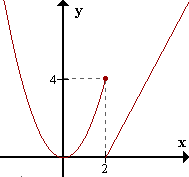 | f(x) = x2 si x <= 2 2x - 4 si x > 2 Discontinua en x=2. Si bien existe f(2), no existe |
Definición
Continuidad por la izquierda
Una función f(x) es continua por la izquierda en el punto a si existe f(a) y limx->a-f(x) = f(a) .
Definición
Continuidad por la derecha
Una función f(x) es continua por la derecha en el punto a si existe f(a) y limx->a+f(x) = f(a) .
La función anterior es continua por la izquierda en x=2, pero no por la derecha.Definición
Continuidad en un intervalo cerrado [a,b]
Una función f(x) es continua en un intervalo cerrado [a,b] si:
f es continua en a por la derecha
f es continua en b por la izquierda
f es continua en x, para todo x perteneciente al intervalo abierto (a,b)
f es continua en a por la derecha
f es continua en b por la izquierda
f es continua en x, para todo x perteneciente al intervalo abierto (a,b)
Clasificación de discontinuidades
Evitable
Caso A:
No existe f(a) pero existe limx->af(x).
Ejemplo:  | f(x)= e-1/x2 + 2 |
limx->0-f(x) = limx->0+f(x) = 2 o sea limx->0f(x)=2
Podemos extender la definición de la función, asignándole en el punto a el valor del límite, con lo cual la función se torna continua. Por ello este tipo de discontinuidad se denomina evitable.
Caso B:
Existe f(a) y existe limx->af(x)=b pero b≠f(a).
(Existe f(a) pero es distinto al valor del límite).
Ejemplo:(Existe f(a) pero es distinto al valor del límite).
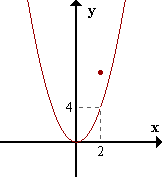 | f(x) = x2 si x≠2 8 si x=2 |
limx->2 f(x) = 4
Asignándole a la función el valor 4 en x=2, se elimina la discontinuidad.
No evitable
1ª especie:
limx->a-f(x) ≠ limx->a+f(x).
(Los límites laterales son distintos).
Ejemplo:(Los límites laterales son distintos).
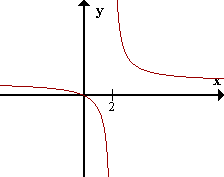 | f(x) = x/(x - 2) |
limx->2+f(x) = +inf
2ª especie:
No existe limx->a-f(x) o no existe limx->a+f(x).
(No existe por lo menos uno de los límites laterales).
Ejemplo:(No existe por lo menos uno de los límites laterales).
 | ______ f(x) = \|x2 - 4 |
Operaciones con funciones continuas
Si f y g son funciones continuas en x=a, la suma, multiplicación y cociente de f y g (con g(a) ≠ 0) son funciones continuas en x=a. H) f(x) es continua en x=a.
g(x) es continua en x=a.
T) f(x) + g(x) es continua en x=a.
Demostración Por definición de continuidad,g(x) es continua en x=a.
T) f(x) + g(x) es continua en x=a.
existe f(a) y existe limx->af(x) = f(a)
existe g(a) y existe limx->ag(x) = g(a)
=> por teo. límite de la suma de funciones, el límite de una suma de funciones es igual a la suma de los límites de cada función, si éstos son finitos.
limx->a f(x) + g(x) = f(a) + g(a)
=> por def. de continuidad f(x) + g(x) es continua en x=a.
Análogamente se prueba la continuidad del producto y el cociente.
Teorema
Continuidad de la función compuesta
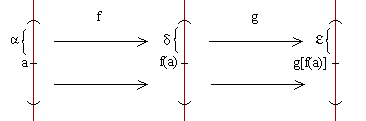
H) f es continua en x=a.
g es continua en x=f(a).
T) g o f es continua en x=a.
Demostración:g es continua en x=f(a).
T) g o f es continua en x=a.
Queremos demostrar que limx->a g[f(x)]=g[f(a)], o sea, por definición de límite, queremos probar que, dado ε>0 existe δ>0 tal que para todo x perteneciente al E*a,δ g[f(x)] perteneciente al Eg[f(a)],ε.
Por hipótesis g es continua en f(a) => por def. de continuidad
para todo x perteneciente al E*f(a),δ g(x) pertenece al Eg[f(a)],ε (1)
Por hipótesis f es continua en a => por def. de continuidad limx->af(x) = f(a), es decir que (por def. de límite) si tomamos el número δ de (1), existe α>0 tal que... para todo x perteneciente al E*a,α f(x) pertenece al Ef(a),δ (2)
De (1) y (2) se deduce que:Dado ε>0 existe α>0 / para todo x perteneciente al E*a,α g[f(x)] pertenece al
Teorema de BolzanoAntes de enunciar el teorema de Bolzano, veamos una definición y una propiedad relativas a sucesiones, que se emplearán en la demostración de dicho teorema. (Por más detalles, visitar la página sobre sucesiones).Definición: Par de sucesiones monótonas convergentes (PSMC) ((an),(bn)) es un PSMC <=> Propiedad: Todo PSMC tiene frontera1) (an) es creciente (bn) es decreciente 2) Para todo n natural an < bn 3) Para todo ε > 0 existe h natural / ((an),(bn)) es un PSMC => existe c / para todo n Teorema de BolzanoBernhard Bolzano (1781-1848) Si una función f(x) es continua en un intervalo cerrado [a,b] y f(a) y f(b) son de distinto signo, existe por lo menos un punto entre a y b para el cual f(c)=0. H) f(x) continua en [a,b] f(a).f(b) < 0 T) Existe c perteneciente a (a,b) / f(c) = 0 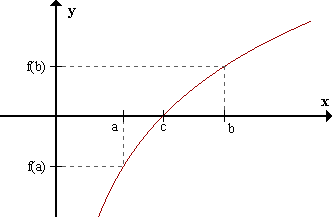 Geométricamente, el teorema establece que si dos puntos (a,f(a)) y (b,f(b)) de la gráfica de una función continua están situados en diferentes lados del eje x, entonces la gráfica intersecta al eje en algún punto entre a y b. Por supuesto que pueden haber varias intersecciones. Geométricamente, el teorema establece que si dos puntos (a,f(a)) y (b,f(b)) de la gráfica de una función continua están situados en diferentes lados del eje x, entonces la gráfica intersecta al eje en algún punto entre a y b. Por supuesto que pueden haber varias intersecciones. Demostración: Supongamos que f(a)<0 y f(b)>0. (La demostración sería análoga si supusiéramos f(a)>0 y f(b)<0.) Consideremos el punto medio de [a,b]: (a+b)/2. Si f((a+b)/2)=0 queda demostrado el teorema. Sino, f será positiva o negativa en (a+b)/2. Tomemos una de las mitades del intervalo [a,b] donde la función sea negativa en un extremo y positiva en el otro. Llamemos a1 y b1 a los extremos de este intervalo. Ahora dividamos [a1,b1] a la mitad. Si f no vale cero en el punto medio, será positiva o negativa. Tomemos la mitad donde f tiene distinto signo en cada extremo, y llamemos a estos puntos a2 y b2. Si continuamos de esta manera, obtenemos una sucesión de intervalos [a,b], [a1,b1], [a2,b2], etc., tales que ![Sucesión de intervalos [an,bn]](http://matematica.50webs.com/graficos/sucint.gif) Es decir, Es decir,1) Los ai forman una sucesión creciente y los bi forman una sucesión decreciente. 2) Los ai son siempre menores que los bi. Veamos cuál es el limn->+inf bn - an. bn - an es la longitud del intervalo [an,bn]. La longitud del intervalo [a1,b1] es (b - a)/2, la mitad de la longitud de [a,b] que es b - a. La longitud del intervalo [a2,b2] es (b - a)/22, la mitad de la longitud de [a1,b1] que es (b - a)/2. Y siguiendo de esta manera, la longitud del intervalo [an,bn] es (b - a)/2n. De modo que, 3) limn->+inf bn - an = limn->+inf (b - a)/2n = 0. 1), 2) y 3) son las condiciones de la definición de PSMC:
((an),(bn)) es un PSMC => existe c / para todo n lim an = c- significa que para todo δ>0 existe n1 / para todo n>=n1 lim bn = c+ significa que para todo δ>0 existe n2 / para todo n>=n2 O sea que tomando el mayor entre n1 y n2, llamémosle n3, se cumplen ambas cosas. Es decir, para todo δ>0 existe n3 / para todo Esto significa que, para cualquier entorno de c que consideremos, existe un intervalo [an,bn] contenido en dicho entorno. 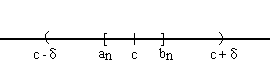 Por otro lado, f es continua en [a,b] por hipótesis. Por lo tanto es continua en c. Por definición de continuidad, limx->c f(x)=f(c). Por otro lado, f es continua en [a,b] por hipótesis. Por lo tanto es continua en c. Por definición de continuidad, limx->c f(x)=f(c). Si f(c)<0, por teo. de conservación del signo existe un entorno de c donde f(x) es negativa. 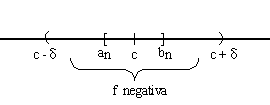 Dentro de este entorno, existe un intervalo [an,bn], donde f(an) es de distinto signo que f(bn). Esto es una contradicción, por lo tanto Dentro de este entorno, existe un intervalo [an,bn], donde f(an) es de distinto signo que f(bn). Esto es una contradicción, por lo tanto Si f(c)>0, por teo. de conservación del signo existe un entorno de c donde f(x) es positiva. Pero, otra vez, dentro de ese entorno existe un intervalo [an,bn] tal que f(an) es de distinto signo que f(bn). Por lo tanto, no existe otra posibilidad: f(c)=0. Propiedad de DarbouxGaston Darboux (1842-1917) Si una función f(x) es continua en un intervalo cerrado [a,b] y k es cualquier número entre f(a) y f(b), entonces existe un valor d entre a y b para el cual f(d)=k. H) f continua en [a,b] f(a) < k < f(b) T) Existe d perteneciente a (a,b) / f(d)=k 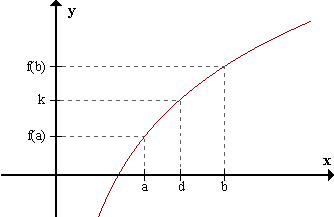 Sea g una función auxiliar: g(x) = f(x) - k. Sea g una función auxiliar: g(x) = f(x) - k.
O sea, existe d perteneciente a (a,b) / f(d)=k.
Fuente:http://matematica.50webs.com/ |
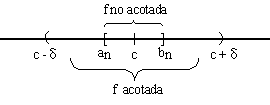 Tenemos pues aquí una contradicción: decimos que f está acotada en
Tenemos pues aquí una contradicción: decimos que f está acotada en